Matematické řešení regulačních obvodů
- Při určování vlastností dynamických členů vyšetřujeme jejich přechodové jevy, které jsou dány závislostí různých veličin na čase, tj. časovými funkcemi.
- Časovou funkci můžeme vyjádřit graficky, jestliže na vodorovnou osu vynášíme čas a na svislou osu vynášíme výstupní nebo vstupní veličinu daného členu.
- Časovou funkci můžeme však také vyjádřit čistě matematicky. Průběh časové funkce je pak určen rovnicí, která ve složitějších případech obsahuje derivace, popř. integrály. Nazýváme ji diferenciální rovnicí.
Derivace časové funkce
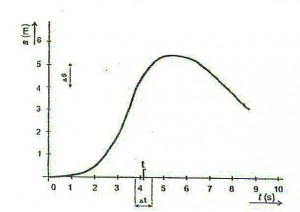
- Na obrázku je znázorněna křivkou derivace časové funkce určující závislost dráhy na čase při nerovnoměrném pohybu.
- Strmost křivky ukazuje, jak rychle se ujetá dráha měnila na čase.
- V libovolném bodě pak z grafu můžeme vyjádřit přibližnou velikost okamžité rychlosti .V okolí zvoleného času si zvolíme malý přírůstek času. Na ose dráhy pak přečteme příslušný přírůstek dráhy.
- Okamžitou rychlost pak přibližně vyjadřuje vztah:
![]()
- Chyba je tím větší, čím větší je zvolený přírůstek času a čím je větší nelineárnost dané časové funkce.
- Abychom zvětšili přesnost, zmenšujeme časový přírůstek. Přírůstek času můžeme zmenšovat např. půlením. Provádíme.li toto půlení neomezeně, dosáhneme stavu, kdy se velikost obou přírůstků blíží nule.Takový přírůstek pak nazýváme diferenciálem.
- Pro diferenciál používáme symbol d.
- Výpočet okamžité hodnoty v čase t při použití diferenciálů je již zcela přesný:
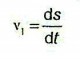
- Výraz určuje derivaci dráhy podle času, zkráceně jej čteme "ds podle dt".
- Fyzikální podstatou první derivace je tedy okamžitá rychlost změny hodnoty derivované veličiny měnící se v čase.
- Je-li veličina konstantní, je rychlost změny nulová a nulová je i její derivace.
- Derivujeme-li danou časovou funkci bod po bodu, získáme časový průběh její změny neboli derivaci jako funkci času.
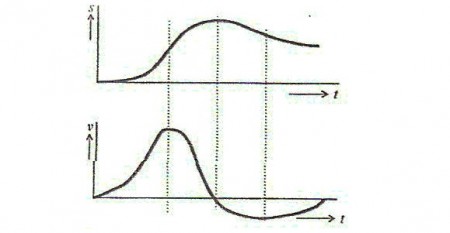
- Rychlost jako funkci času můžeme opět derivovat, čímž získáme "rychlost změny rychlosti" neboli zrychlení původní veličiny.
- V našem případě můžeme vyjádřit zrychlení jako funkci času derivací rychlosti nebo druhou derivací dráhy:
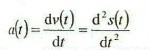
- Poslední výraz čteme jako "d druhé s podle dt na druhou".
- Fyzikální podstatou druhé derivace je tedy zrychlení dané veličiny v určitém čase t.
- Geometrický význam derivace: Ze vztahu pro zrychlení je zřejmé, že hodnota derivace v kterékoliv bodě funkční křivky je dána strmostí této křivky.
- Stoupá-li křivka, je derivace kladná.
- Nemění-li se hodnota dané veličiny s časem, je derivace nulová.
- Jestliže křivka klesá, je derivace záporná.
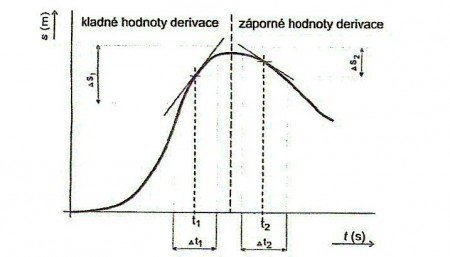
- Strmost křivky můžeme definovat sklonem tečny zkonstruované v kterémkoliv bodě funkční křivky.
- Tangens úhlu, který tečna svírá s kladnou částí časové osy, nazýváme směrnicí tečny.